Величина коэффициента эластичности показывает – 2.Величина коэффициента эластичности показывает:

Содержание

2.Величина коэффициента эластичности показывает:

Что понимается под адекватностью модели:

1) Остаточная компонента Е удовлетворяет 4-м условиям, сформулированным в теореме Гаусса-Маркова и соответствие модели наиболее важным (для исследователя) свойствам.

1) На сколько % изменится в среднем результат при изменении фактора на 1%.

3.Когда используется метод инструментальных переменных:

1)… большими ошибками или вообще неизмерима, но может заменяться другой объясняющей переменной или если объясняющая переменная измерима, но коррелирует существенным образом со случайной составляющей.

4.МНК используется для оценивания:

1)параметров линейной регрессии.

5.Коэффициент детерминации рассчитывается для оценки качества:

1)параметров уравнения регрессии.

6.Критическое значение критерия Стьюдента определяется по:

1) уровню значимости и одной степени свободы.

7.Как определить наличие мультиколлинеарности между факторными признаками уравнения регрессии:

1)Путем расчета матрицы коэффициентов парной корреляции.

8.В каких случаях для определения параметров системы одновременных уравнений применяется трехшаговый метод наименьших квадратов:

1) Если коэффициенты системы одновременных уравнений связаны между собой дополнительными связями или имеет 3-е уравнение, связывающие эндогенные переменные между собой.

9.Эконометрика-это

1) наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.

10.Ошибки второго рода- это ошибки

1) Имеющие объективный характер.

11.Метод Кокрана- Оркатта, используемый для оценки коэффициента автокорреляции и коэф-в уравнения регрессии, вкл. следущие этапы:

1) …7 пунктов.

12.Несмещенность оценки характеризуется…

1) —равенством нулю математического ожидания остатков

—отсутствием накопления остатков при большом числе выборочных оцениваний

13.Какаи наборы статистических показателей используется для оценки точности модели:

1) Среднеквадратическое отклонение, средняя относительная ошибка аппроксимации, коэф-т сходимости, коэф-т множественной детерминации.

14. Для чего используется поправка Прайса- Уинстена:

1) Для дисбаланса, связанного с неоправданно большим влиянием первого наблюдения на определяемые оценки параметров уравнения при применении МНК.

15.Среднеквадратические ошибки асимметрии и эксцесса характеризуют:

1)Фактическую величину асимметрии и эксцесса в конечной выборке.

16. Величина коэф-та парной корреляции хар-т предельный допустимый уровень мультиколлинеарности между факториальными признаками уравнения регрессии:

1) 0,8

17.Коэф-т парной корреляции показывает:

1)Силу влияния отдельного факториального признака Х на величину У при условии, что остальные факторы остаются неизменными.

18. В стационарном временном ряде трендовая компонента

1)отсутствует

19.При выполнении предпосылок МНК оценки параметров регрессии обладают свойствами:

–эффективность.

— несмещенность.

-состоятельность.

20. В методе Койка уменьшение во времени лаговых воздействий фактора на результат описывается формулой

1) –bj = b0* лямдуt 0<лямда<1

— bj= c0+c1^2+c2^3*j

21. Какое основное отличие корреляционной зависимости Y=f(x) от функциональной:

1)Каждому значению X соответствует ряд распределения Y.

22. Какие системы алгебраических уравнений называются системами одновременных уравнений:

1) Системы уравнений, в которых одни и те же переменные в одних уравнениях как объясняющие, а в других в качестве объясняемых.

23. С помощью традиционного МНК нельзя определить параметры уравнений, входящих в систему_______ уравнений

1)одновремённых

24. Приведённое уравнение регрессии вида у=а+в*х^а+и можно линеаризовать путём:

1)нельзя линеаризовать.

25. По какой формуле определяется доверительный интервал для отдельных коэф-ф уравнения регрессии:

1) (а_j–r_aj*t_кр)<= а_j <= (а_j+ r_aj*t_кр)

26. Автокорреляция случайного члена уравнения регрессии приводит к тому, что оценки уравнения регрессии становятся:

1)неэффективными.

27. Что означает состоятельность МНК- оценки параметров уравнения регрессии:

1)Дисперсия оценок параметров при росте числа наблюдений в выборке стремиться к 0.

28. В тесте Чоу F-статистика определяется по формуле:

1) F=(U_P-U_A-U_B)*(p+1)

(U_A+U_B)/(n-2p-2)

29.Выберите верные утверждения по поводу системы одновременных уравнений:

1) Может быть представлена в структурной форме модели и в приведенной форме.

2) В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях- в правую часть системы.

30. Припроверке соответствия распределения случайной компоненты нормальному закону распределения:

1) Используются показатели асимметрии и эксцесса.

31. Случайная компонента трендовой модели должна обладать свойствами:

1)Мат.ожидание равно 0, отсутствии автокорреляции, случайность колебаний, соответствие нормальному закону распределения.

32. В общем случае временной ряд показателей максимально можно разложить на:

1) Трендовую составляющую, сезонную составляющую, циклическую и случайную составляющую.

33. Поправка Прайса- Уистена равна:

1) к=(1-р²)^0,5

34. При обсуждении существенности параметра регрессии рассматривается нулевая статистическая гипотеза о(об)____ оценки этого параметра:

1)равенстве 0.

35.Чем характеризуется множественная регрессия:

1) Множеством факториальных признаков.

36. Оценка адекватности и точности регрессионного уравнения, связывающего изучаемый экономический показатель с выбранными факторами-аргументами, называется:

1) Верификацией уравнения регрессии.

37. Что характеризует коэф-т множественной корреляции:

1) Долю изменения У, которую можно изменить изменением включенным в модель факторов.

38. Эндогенные переменные…

1) могут коррелировать с ошибками регрессии

39. Временным рядом является совокупность значений

1) экономического показателя за несколько последовательных моментов (периодов) времени.

40. Анализ возможности численной оценки неизвестных коэффициентов структурных уравнений по оценкам коэф-в приведенных уравнений составляет

1)проблема идентификации.

41. Этап корреляционного анализа, на котором определяются формы связи изучаемого экономического показателя с выбранными факторами-аргументами, имеет название

1) Спецификация модели

42. В чем заключается суть метода инструментальных переменных:

1) В частичной замене непригодной объясняющей переменной такой переменной, которая существенным образом отражает воздействие на результирующую переменную исходной объясняющей переменной, но коррелирует со случайной составляющей

43. Определить в какой системе уравнений находиться неидентифицируемое уравнение регрессии:

1) С_t=а+в*У_t+u_t; У_t=С_t+I_t

44. Формула для определения значения уровня временного ряда при использовании экспоненциального сглаживания имеет вид:

1) у_t=а*у_t+(1-а)*у_t_-1

45. Экономическая модель, являющаяся системой одновременных уравнений состоит в общем случае

1) из поведенческих уравнений и тождеств

46. Выберите верные утверждения по поводу системы одновременных уравнений:

1) Может быть представлена в структурной форме модели и в приведенной форме

2) В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других- в правую часть системы.

47.В линейном уравнении парной регрессии у=a+bx+E переменными не являются:

-а, -b.

48. Что понимается под показателями, характеризующие точность модели:

1) Разность между значениями фактических уровней ряда и их теоретическими уровнями, оцениваемыми с помощью статистических показателей.

49.Под аномальным уровнем временного ряда понимается:

1) Отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и, оставаясь в качестве уровня ряда, оказывает существенное влияние на значение основных показателей.

50.Значение коэф-та корреляции равно 0,81. Можно сделать вывод о том, что связь между результативным признаком и фактором является:

1)достаточно тесной.

51.Формула для определения сглаженного значения уровня временного ряда при использовании скользящей средней имеет вид:

1)У=сумм У_tр=m-1

m 2

52.Значение d-критерия статистики Дарбина-Уотсона в больших выборках связано с коэф-м автокорреляции случайного члена уравнения регрессии приближенно следующим соотношениям:

1)d_p=2-2p

53.Что понимается под дисперсией случайного члена уравнения регрессии:

1) Возможное поведение случайного члена уравнения регрессии до того, как сделана выборка.

54.Выберите счетное формальное правило, отражающее необходимое условие идентифицируемости уравнений, входящих в систему одновременных уравнений:

1)Н=D+1

55.В каком случае нельзя отклонить нулевую гипотезу об отсутствии автокорреляции случайного члена уравнения регрессии:

1)Если расчетное значение критерия d попадает в зону неопределенности.

56.В каких случаях используется тест Чоу:

1)При решении вопроса о целесообразности разделение выборки на две подвыборки и построение, соответственно, двух регрессионных моделей.

57.Нелинейным считается уравнение регрессии нелинейное относительно входящих в него:

1)параметров.

58.Причиной положительной автокорреляции случайного члена уравнения регрессии обычно является:

1)Постоянная направленность воздействия не включенного в уравнение регрессии какого-либо фактора.

59.Что является предметом эконометрики:

1)Факторы, формирующие развитие экономических явлений и процессов.

60.Ошибки первого рода устраняются путем:

1)Замены аномального наблюдения средней арифметической двух соседних уровней ряда.

61.Фиктивная переменная может принимать значения:

1)0, 2)1

62.Согласно тесту ранговой корреляции Спирмена нулевая гипотеза об отсутствии гетероск-ти случайного члена уравнения регрессии будет отклонена при уровне значимости 5%, если тестовая статистика:

1)Будет больше 1,96

63.Корреляция подразумевает наличие связи между:

1)переменными

64.Отбор факторов в экономическую модель множественной регрессии может быть осуществлен на основе:

1)Матрицы парных коэф-ф корреляции.

65. Как устранить автокорреляцию случайных членов уравнения регрессии, если она описывается авторегрессионной схемой первого порядка:

1)Необходимо исключить из уравнения регрессии все факторы, вызывающие автокорреляцию.

66.Что понимается под «совершенной мультиколлинеарностью» объясняющих переменных в уравнении регрессии:

1)Функциональную связь друг с другом объясняющих переменных в уравнении регрессии.

67.КМНК применим для:

1)идентифицируемой системы одновременных уравнений.

68. Эконометрическая модель-это

1)экономическая модель, представленная в математической форме

69.С использованием какой формулы можно вычислить коэф-т парной корреляции:

1)r_x,y=

Cov(x,y)

(Var(x)*Var(y))^0,5

70.Эффективность МНК- оценки параметров уравнения регрессии означает что:

1)Оценки имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров.

71.Стохастический стационарный в слабом смысле процесс, включая временной ряд, независимо от рассматриваемого периода времени и длины лага между рассматриваемыми переменными, имеет постоянную величину:

-дисперсии процесса

-среднего значения процесса.

72.Какие переменные считаются предопределенными переменами:

1)Это экзогенные и лаговые переменные.

73.Метод Хилдреда-Лу , используемый для оценки коэф-та автокорреляции случайного члена уравнения регрессии и коэф-в самого уравнения регрессии, заключается в следующем:

1)Задаем интервал изменения р и величину р. Для каждого значения р производится оценка параметра  и  из приведенной системы уравнений ^’_t=C+Xt^’+_t. Затем из полученных результатов выбирается тот, к-й дает минимальную стандартную ошибку. Эти значения р,  и  принимаются за искомые.

74.Распределение остаточной компоненты _i=_i—_i^’ в генеральной совокупности подчиняется нормальному закону. Это позволяет:

1) Признать гипотезу о неслучайном характере отклонений уровней ряда от теоретических уровней.

75.Проверка по d-критерию Дарбина-Уотсона производится путем сравнения:

1)Расчетное значение критерия d^’ с верхним d₂ и нижним d₁ –критическими значениями статистики Дарбина-Уотсона.

76.Выбор мультипликативной модели временного ряда производится, если сезонные колебания имеют:

1)возрастающую или уменьшающую амплитуду колебаний.

77.При нахождении распределительного лага методом Алмона необходимо иметь предварительную информацию:

-о величине лага

-о степени полинома, описывающего структуру лага.

78.Укажите причину, по которой нельзя составить таблицу с указанием точных критических значений d-критерия статистики Дарбина-Уотсона:

1) d-критерий статистики Дарбина-Уотсона зависит от масштаба переменных в уравнении регрессии.

79.Фиктивные переменные в уравнении множественной регрессии являются:

1)качественные переменные, преобразованные в количественные.

80.Какие коэф-ты показывают силу влияния на результирующий признак отдельных факторов и их совокупное влияние?

1)Коэф-ты множественной, парной и частной корреляции

81. Время как замещающая переменная в функции Кобба-Дугласа используется для

1)Учета изменения параметров производственной функции через показатель научно-технического прогресса.

82.Для зависимости спроса на некоторый товар от цены за единицу товара и дохода потребителя получено уравнение регрессии вида у=а+b₁+x₁+b₂+x₂+. Парными коэф-ми корреляции могут быть:

—r_x_1,_x_2, —r_y_,_x_1.

83. Этот показатель вычисляется по результатам анкетного опроса широкого круга специалистов:

1)Сумма рангов

84. К видам экономических моделей по типам зависимости относятся модели:

-линейной регрессии, -нелинейной регрессии.

85.Величина коэф-та регрессии показывает:

1)среднее изменение результата при изменении фактора на одну единицу

86.Какие уравнения называются уравнениями в приведенной форме:

1)Это уравнения, в которых эндогенные переменные выражаются через предопределенные переменные и случайные составляющие.

87.Что проверяется при использовании теста, основанного на критерии серий:

1)С помощью теста основанного на критерии серии можно проверить гипотезу о случайном характере отклонений уровней ряда от теоретических уровней.

88.Закон сложения дисперсий для линейного уравнения регрессии имеет вид:

1)_у²=_у²+_е²

89.Применение КМНК возможно для идентифицируемой системы одновременных уравнений, т.к в идентифицируемых системах:

1)возможно однозначное выражение коэф-в структурной формы через коэф-ты приведенной формы системы.

90. Предпосылками метода наименьших квадратов являются:

-мат ожидание случайных отклонений =0;

-дисперсия случайных отклонений постоянна для всех наблюдений;

-случайные отклонения являются независимыми друг от друга.

91.Предпосылками МНК являются следующее:

—гомоскедастичность; -отсутствие автокорреляции остатков.

92.Какие основные экономические задачи решаются с использованием эконометрики:

1)Процесс принятия управленческих решений.

93.В экономических моделях с m независимыми переменными наблюдаемые значения зависимой переменной У_1,отличается от модельных У₁^’на величину е_i_.В данных обозначениях формула для расчета оценки общей дисперсии зависимой переменной D_общ имеет вид:

1) D_общ=сумм e_i²

n—m-1

94.Для степенной регрессионной модели вида: У_i=а+b₁X_i+b₂X_i²+b₃X_i³возможен аддитивный способ включения случайного возмущения. Для получения качественных оценок параметров этой модели:

1)необходимо выполнить логарифмическое преобразование.

95.При обсуждении существенности параметра регрессии рассматривается нулевая статистическая гипотеза о (об) ______ оценки этого параметра.

1)равенстве 0.

96.Пусть t-рассчитанная для коэф-та статистики Стьюдента, а t_кр–критическое значение этой статистики. Коэф-т регрессии считается статистически значимым, если выполняются следующие неравенства:

1) t_кр< t; 2) —t_кр> t_.

97. С помощью подходящих преобразований исходных переменных регрессионная зависимость представляется в виде линейного соотношения между преобразованными переменными:

1)оптимизация

98.Значение коэф-та детерминации составило 0,9. Следовательно отношение ___ дисперсии к общей равно____.

1)остаточной….0,1 2)факторной …0,9

99.Ошибки первого рода – это ошибки

1)Технического порядка.

100.Тестовая статистика в тесте ранговой корреляции Спирмена определяется по формуле:

1)t_расч=r_x_,|_e_|*n-1

101.Гетероскедастичность-это

1)Явление, когда с изменением факториального признака(Х) дисперсия случайной компоненты будет монотонно увеличиваться или уменьшаться, или изменяться по какому-либо другому закону.

102.Гомоскедастичность подразумевает:

1)одинаковую дисперсию остатков при каждом значении факторов.

103.Случайная компонента трендовой модели должна обладать свойствами:

1)Мат.ожидание равно 0, отсутствие автокорреляции, случайность колебаний, соответствие нормальному закону распределения.

104.ОМНК подразумевает:

1)введение в выражение для дисперсии остатков коэф-та пропорциональности

2)преобразование переменных

105.Зависимость валового национального продукта(У) от денежной массы(Х) характеризуется линейно-логарифмической экономической моделью, имеет вид:

1)У=а₀+а₁*LnX+

106.Если наличие существенной гетероскедастичности случайного члена уравнения регрессии подтверждено тестами, то для снижения влияния гетескедастичности на эф-ть оценок уравнения регрессии необходимо:

1)Разделить каждый член уравнения регрессии в каждом наблюдении на дисперсию случайной составляющей.

107.Что представляют собой в тесте, основанном на критерии серий, величины: К=[3,3*lg(n+1)] и v=[1/2*(n+1-1,96*n-1)].

1)Данные величины представляют собой расчетные допустимые значения максимальной длины серии и общего числа серий соответственно.

108.В ДМНК при применении его к системе одновременных уравнений в качестве второго шага выполняются следующие процедуры:

1)Находят теоретические значения эндогенных переменных, и эти значения подставляют в исходную систему одновременных уравнений вместо фактических значений эндогенных переменных в правой части уравнения и определяют оценки параметров уравнения регрессии.

109.Каковы причины использования замещающих переменных:

1)Показатели, включаемые в уравнение регрессии, имеют расплывчатые определения и их нельзя измерить, либо требует для своего измерения очень много времени и средств

110. В эконометрических моделях с m неизвестными переменными наблюдаемые значения зависимой переменной Уi , отличается от модельных Уi (теор) на величину эпсилат .в данных обозначениях формула для расчета Суммы кВ. откл =

1) Сумма (Уi{теор} –Yi {средн })^2

111. Что такое «Несовместные системы уравнений»

1) точное решение одной системы уравнений не удовлетворяет другим уравнениям.

112. Нахождение тренда временного ряда аналитического выравнивания включает в себя этапы:

1) спецификации, параметризации и последующей верификации различных функций.

113. К видам эконометрических моделей по типам зависимости относятся модели:

1)линейной регрессии, нелинейной регрессии.

114. В чем заключается метод отбора исходных данных «заводо-лет»:

1) Отбор исходных данных о работе предприятий отрасли за несколько смежных лет.

115. Под автокорреляцией уравнения временного ряда подразумевается:

1) корреляционная зависимость между последовательными уравнения временного ряда.

116. К видам эконометрических моделей по типам зависимости относятся модели:

1)Fp>Fm

117. Расчетное значение d – критерия статистики Дарбина — Уотсона определяется по формуле:d = сумма (Еi –Ei-1)^2/ сумма Ei^2

i=2 i=2

118. Коэффициент парной корреляции характеризует:

1) тесноту линей связи между двумя переменными.

119. Гипотеза о нормальном распределении случайной компоненты принимается, если выполняются неравенства:

;

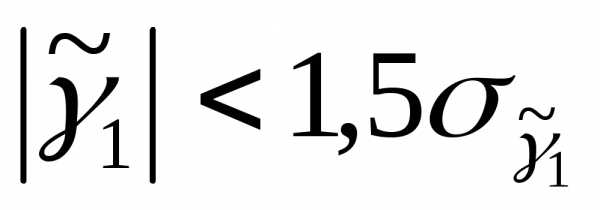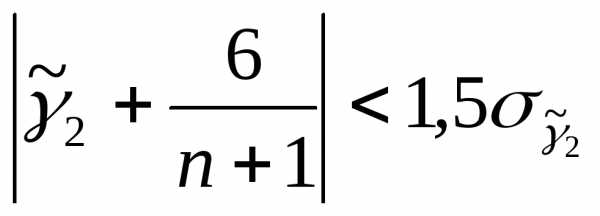
120. В эконометрических моделях с m неизвестными переменными наблюдаемые значения зависимой переменной Уi , отличается от модельных Уi (теор) на величину эпсилат .в данных обозначениях формула для расчета оценки общей дисперсии зависимой переменно D имеет вид:

1) D= сумма (Yi—Y{среднее})^2 / n-1

121. Что понимается под трендом временного ряда:

1) изменение уравнений временного ряда, определяющее общее направления развития, основную тенденцию временного ряда.

другие с прошлого года.

1) что является предметом эконометрии?

1) факторы, формирующие развитие экономических явлений и процессов.

2) факторы, формирующие развитие физических явлений и процессов

3) факторы, формирующие развитие химических явлений и процессов

2)Какие основные экономические задачи решаются с использованием эконометрии?

1) является прогнозирование путей развития макро- и микроэкономических факторов хозяйственной деятельности.

2) является прогнозирование путей развития макро- и мегаэкономических факторов хозяйственной деятельности

3) является прогнозирование путей развития мега- и микроэкономических факторов физической деятельности

3)Какие основные методы используются при построении экономических моделей?

1) метод регрессионного и корреляционного анализа.

2) метод статики и динамики

3) метод дедукции и индукции

4)Какое основное отличие корреляционной зависимости y=f(x) от функциональной?

1) При функциональной зависимости каждому аргументу (X) соответствует строго определённое значение (У), а при корреляционной зависимости- каждому аргументу (X) соответствует не одно строго определённое значение функции (У), а ряд распределения этой величины.

2) При корреляционной зависимости каждому аргументу (X) соответствует строго определённое значение (У), а при функциональной зависимости- каждому аргументу (X) соответствует не одно строго определённое значение функции (У), а ряд распределения этой величины.

3) Отличия нет

5. Что показывает линия регрессии?

1) количественную связь факторных признаков изучаемого явления;

2) как в среднем изменяется У с изменением Х;

3) наиболее важные характеристики изучаемого объекта или явления.

6. Чем характеризуется множественная регрессия?

1) множеством факторных признаков;

2) множеством результативных и факторных признаков;

3) одним факторным признаком.

7. Что такое «несовместная система уравнений»?

1) система уравнений, в которой точное решение какого-либо уравнения системы удовлетворяет остальным уравнениям;

2) система уравнений, в которой точное решение какого-либо уравнения системы невозможно найти;

3) система уравнений, в которой точное решение какого-либо уравнения системы не удовлетворяет остальным уравнениям.

8. В чём заключается принцип наименьших квадратов?

1) наивероятнейшими значениями параметров уравнения регрессии будут такие, при которых сумма квадратов отклонений будет наибольшая;

2) наивероятнейшими значениями параметров уравнения регрессии будут такие, при которых сумма отклонений будет наименьшая;

3) наивероятнейшими значениями параметров уравнения регрессии будут такие, при которых сумма квадратов отклонений будет наименьшая.

9. Каким образом находятся параметры aj из системы уравнений

(1)

1.Наивероятнейшими значениями параметров aj будут такие значения при которых сумма квадратов отклонений будет минимальна. Для нахождения минимума функции 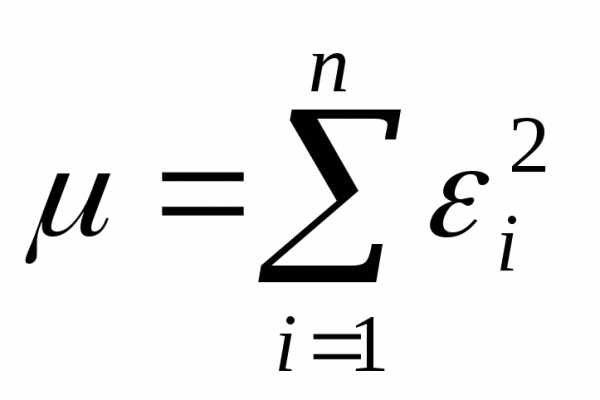необходимо взять частную производную по уравнению (1) по параметру aj и приравнять ее к 0

2. Наивероятнейшими значениями параметров ajбудут такие значения при которых сумма квадратов отклонений будет максимальна. Для нахождения максимума функции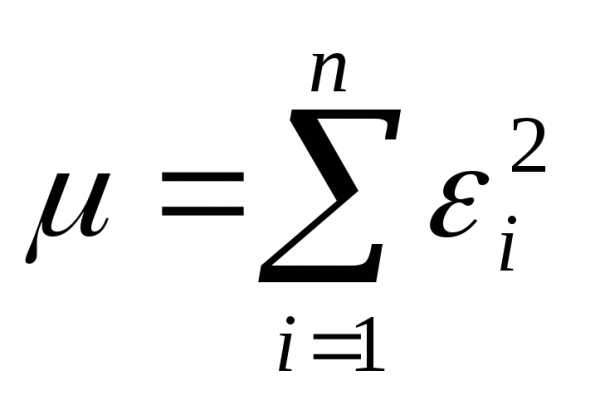необходимо взять частную производную по уравнению (1) по параметруajи приравнять ее к 1

3. Наивероятнейшими значениями параметровajбудут такие значения при которых сумма квадратов отклонений будет максимальна. Для нахождения максимума функции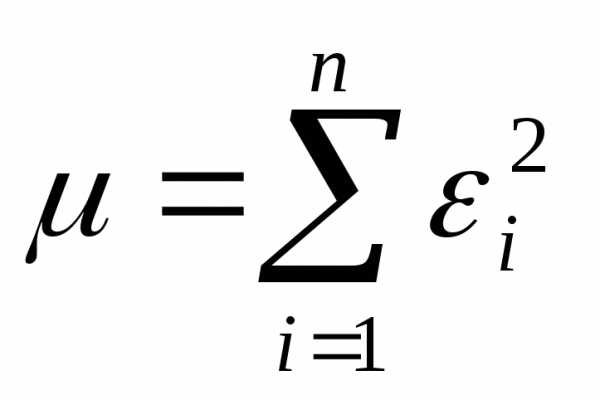необходимо взять частную производную по уравнению (1) по параметруajи приравнять ее к 0.

studfiles.net

Тест: Ответы на тест по эконометрике

Тема: Ответы на тест по эконометрике

Раздел: Бесплатные рефераты по эконометрике

Аддитивная модель содержит компоненты в виде …

комбинации слагаемых и сомножителей

сомножителей

отношений

слагаемых

В линейной регрессии Y=b0+b1X+e параметрами уравнения регрессии являются: (неск)

В правой части приведенной формы системы одновременных уравнений, построенной по перекрестным данным (cross-section data) без учета временных факторов, могут стоять _______ переменные.

лаговые

зависимые

эндогенные

экзогенные

В стационарном временном ряде трендовая компонента …

имеет линейную зависимость от времени

отсутствует

имеет нелинейную зависимость от времени

присутствует

Величина коэффициента детерминации … (неск)

характеризует долю дисперсии зависимой переменной y, объясненную уравнением, в ее общей дисперсии

рассчитывается для оценки качества подбора уравнения регрессии

характеризует долю дисперсии остаточной величины в общей дисперсии зависимой переменной у

оценивает значимость каждого из факторов, включенных в уравнение регрессии

Величина коэффициента регрессии показывает …

среднее изменение фактора при изменении результата на одну единицу измерения

на сколько процентов изменится результат при изменении фактора на 1 %

значение тесноты связи между фактором и результатом

среднее изменение результата при изменении фактора на одну единицу измерения

Величина коэффициента эластичности показывает …

на сколько процентов изменится в среднем результат при изменении фактора на 1%

во сколько раз изменится в среднем результат при изменении фактора в два раза

предельно допустимое изменение варьируемого признака

предельно возможное значение результата

Временным рядом является совокупность значений …

экономического показателя за несколько последовательных моментов (периодов) времени

последовательных моментов (периодов) времени и соответствующих им значений экономического показателя

экономических однотипных объектов по состоянию на определенный момент времени

экономического показателя для однотипных объектов на определенный момент времени

Выберите верные утверждения по поводу структурной формы системы эконометрических уравнений:

каждое уравнение системы может рассматриваться в качестве отдельного уравнения регрессии зависимости одной переменной от группы факторов

система регрессионных уравнений, матрица коэффициентов которых симметрична

эндогенные переменные в одних уравнениях могут выступать в роли независимых переменных в других уравнениях системы

система одновременных уравнений описывает реальное экономическое явление или процесс

Гомоскедастичность остатков подразумевает …

рост дисперсии остатков с увеличением значения фактора

максимальную дисперсию остатков при средних значениях фактора

уменьшение дисперсии остаток с уменьшением значения фактора

одинаковую дисперсию остатков при каждом значении фактора

Диаграмма рассеяния указывает на нелинейную зависимость. В этом случае следует осуществить … (неск)

расчет линейного коэффициента корреляции и использование линейной модели

включение в модель дополнительных факторных признаков

визуальный подбор функциональной зависимости нелинейного характера, соответствующего структуре точечного графика

подбор преобразования переменных, дающего наибольшее по абсолютной величине значение коэффициента парной корреляции

Для линейного уравнения регрессии у = а + bx + e метод наименьших квадратов используется при оценивании параметров…(неск)

Для расчета критического значения распределения Стьюдента служат следующие параметры:

количество зависимых переменных

объем выборки и количество объясняющих переменных

коэффициент детерминации

уровень значимости

К классам эконометрических моделей относятся: (неск)

системы нормальных уравнений

корреляционно – регрессионные модели

модели временных рядов

автокорреляционные функции

Компонентами временного ряда являются: (неск)

циклическая (сезонная) компонента

коэффициент автокорреляции

лаг

тренд

Корреляция подразумевает наличие связи между …

результатом и случайными факторами

переменными

случайными факторами

параметрами

Косвенный метод наименьших квадратов применим для …

неидентифицируемой системы уравнений

неидентифицируемой системы рекурсивных уравнений

любой системы одновременных уравнений

идентифицируемой системы одновременных уравнений

Коэффициент детерминации рассчитывается для оценки качества…

подбора уравнения регрессии

параметров уравнения регрессии

факторов, не включенных в уравнение регрессии

мультиколлинеарных факторов

Коэффициент парной корреляции характеризует тесноту ____ связи между _____ переменными.

нелинейной … несколькими

линейной … несколькими

нелинейной … двумя

линейной … двумя

Критические значения критерия Стьюдента определяются по…

двум степеням свободы

уровню незначимости

трем и более степеням свободы

уровню значимости и одной степени свободы

Метод наименьших квадратов используется для оценивания …

величины коэффициента детерминации

параметров линейной регрессии

величины коэффициента корреляции

средней ошибки аппроксимации

Нелинейным является уравнение регрессии нелинейное относительно входящих в него …

параметров

случайных величин

результатов

факторов

Несмещенность оценки характеризует …

равенство нулю математического ожидания остатков

наименьшую дисперсию остатков

ее зависимость от объема выборки

увеличение точности ее вычисления с увеличением объема выборки

Обобщенный метод наименьших квадратов применяется в случае…

фиктивных переменных

мультиколлинеарности факторов

автокорреляции переменных

автокорреляции остатков

Под автокорреляцией уровней временного ряда подразумевается _____ зависимость между последовательными уровнями ряда.

корреляционно–функциональная

функциональная

детерминированная

корреляционная

При выполнении предпосылок МНК оценки параметров регрессии обладают свойствами: (неск)

достоверность

несостоятельность

несмещенность

эффективность

Предпосылками МНК являются … (неск)

случайные отклонения коррелируют друг с другом

гетероскедастичность случайных отклонений

случайные отклонения являются независимыми друг от друга

дисперсия случайных отклонений постоянна для всех наблюдений

Примерами фиктивных переменных могут служить: (неск)

возраст

доход

пол

образование

Примером нелинейной зависимости экономических показателей является …

зависимость объема продаж от недели реализации, выраженная линейным трендом

линейная зависимость затрат на производство от объема выпуска продукции

линейная зависимость выручки от величины оборотных средств

классическая гиперболическая зависимость спроса от цены

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками…

однородности выборочной совокупности

оценивания параметров

спецификации модели

определения случайных воздействий

Система эконометрических уравнений включает в себя следующие переменные:

системные

эндогенные

случайные

экзогенные

Способами определения структуры временного ряда являются: (неск)

анализ автокорреляционной функции

расчет коэффициентов корреляции между объясняющими переменными

построение коррелограммы

агрегирование данных за определенный промежуток времени

Среди нелинейных эконометрических моделей рассматривают следующие классы нелинейных уравнений: …

внешне нелинейные

внешне линейные

внутренне нелинейные

внутреннее линейные

Структурной формой модели называется система ____ уравнений.

фиксированный

взаимосвязанных

независимых

рекурсивных

Тенденция временного ряда характеризует совокупность факторов, …

оказывающих сезонное воздействие

оказывающих единовременное влияние

оказывающих долговременное влияние и формирующих общую динамику изучаемого показателя

не оказывающих влияние на уровень ряда

Укажите верные характеристики коэффициента эластичности:

коэффициент эластичности показывает на сколько процентов изменится значение результирующего фактора при изменении на один процент объясняющего фактора

коэффициент эластичности является постоянной величиной для всех видов моделей

коэффициент эластичности показывает на сколько изменится значение результирующего фактора при изменении объясняющего фактора на одну единицу

по значению коэффициента эластичности можно судить о силе связи объясняющего фактора с результирующим

Укажите последовательность этапов оценки параметров нелинейной регрессии Y = a + b*X + c*X².

3 оцениваются параметры регрессии b0, b1, b2

1 выполняется замена переменной X2 на Z

2 задается спецификация модели в виде Y = b₀ + b₁*X +b₂*Z, где b₀= a; b₁ = b; b₂ =c

4 определяются исходные параметры из тождеств: a = b₀; b = b₁; c = b₂

Укажите последовательность этапов проведения теста Голдфелда-Квандта для парной линейной регрессии.

4 вычисление статистики Фишера

1 упорядочение наблюдений по возрастанию значений объясняющей переменной

3 оценка сумм квадратов отклонений для регрессий по k-первым и k-последним наблюдений

2 оценка регрессий для k-первых и k-последних наблюдений

Укажите справедливые утверждения по поводу критерия Дарбина-Уотсона: (неск)

позволяет проверить гипотезу о наличии автокорреляции первого порядка

изменяется в пределах от 0 до 4

равен 0 в случае отсутствия автокорреляции

применяется для проверки гипотезы о наличии гетероскедастичности остатков

Укажите существующие классы эконометрических систем: (неск)

система нормальных уравнений

система стандартных уравнений

система одновременных уравнений

система независимых уравнений

Укажите требования к факторам, включаемым в модель множественной линейной регрессии: (неск)

между факторами не должна существовать высокая корреляция

факторы должны быть количественно измеримы

факторы должны иметь одинаковую размерность

факторы должны представлять временные ряды

Установите соответствие между названием модели и видом ее уравнения:

1. линейная

2. полиномиальная

3. показательная

4. полулогарифмическая

4 у = а*lnx*e;

2 y = a + bx + cx² + e;

3 y = ab^x*e;

1 y = a + bx + e

Установите соответствие между наименованиями элементов уравнения Y=b0+b1X+e и их буквенными обозначениями:

1. параметры регрессии

2. объясняющая переменная

3. объясняемая переменная

4. случайные отклонения

3 Y

4 e

1 b0, b1

2 X

Установите соответствие между эконометрическими терминами и их определениями.

1. автокорреляция уровней временного ряда

2. коэффициент автокорреляции уровней временного ряда

3. автокорреляционная функция

4. коррелограмма

3 последовательность коэффициентов автокорреляции первого, второго и т.д. порядков

4 график зависимости значений автокорреляционной функции от величины лага

1 корреляционная зависимость между последовательными уровнями ряда

2 коэффициент линейной корреляции между последовательными уровнями

Фиктивными переменными в уравнении множественной регрессии являются …

качественные переменные, преобразованные в количественные

комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели

переменные, представляющие простейшие функции от уже включенных в модель переменных

дополнительные количественные переменные, улучшающие решение

Число степеней свободы общей, факторной и остаточной дисперсий связано …

только с числом единиц совокупности

с числом единиц совокупности и видом уравнения регрессии

характером исследуемых переменных

только с видом уравнения регрессии

Число степеней свободы связано с числом … (неск)

единиц совокупности (количеством наблюдений)

фиктивных переменных

видом уравнения регрессии

случайных ошибок

Эконометрика – это …

раздел экономической теории, связанный с анализом статистической информации

специальный раздел математики, посвященный анализу экономической информации

наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов

наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Тесты на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Тесты для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Если Тест, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавить отзыв могут только зарегистрированные пользователи.

studrb.ru

48. Коэффициенты эластичности. Ответы на экзаменационные билеты по эконометрике

48. Коэффициенты эластичности

Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле:

где

– первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня

если факторная переменная х изменится на 1 % относительного своего среднего уровня

Общая формула для расчёта коэффициента эластичности для среднего значения

факторной переменной х:

где

– значение функции у при среднем значении факторной переменной х.

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

yi=?0+?1xi,

средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Это единственная нелинейная функция, для которой средний коэффициент эластичности

равен коэффициенту регрессии ?1.

Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1.

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1, если факторная переменная изменится на 1 % относительно заданного уровня х1.

Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:

Для линейной функции вида:

yi=?0+?1xi,

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение линейной функции в точке х1.

Для полиномиальной функции второго порядка (параболической функции) вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение параболической функции в точке х1.

Для показательной функции вида:

точечный коэффициент эластичности определяется по формуле:

Для степенной функции вида:

точечный коэффициент эластичности определяется по формуле:

Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

через первую производную результативной переменной по заданной факторной переменной x1:

Следовательно, Э(x1) = ?1, что и требовалось доказать.

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.

Поделитесь на страничке

Следующая глава >

info.wikireading.ru

46.Содержательная интерпретация коэффициентов степенной регрессионной модели

К классу степенных функций относятся кривые спроса и предложения, кривые Энгеля. Если степенная функция отражает зависимость объема выпуска продукции y от использования ресурса x ( в которой 0<<1), то она называется производственной функцией. Например, производственная функция Кобба-Дугласа связывает объем производства Y с затратами капитала K и затратами труда L: Y=A. Автономная зависимость от времени выражена в коэффициенте научно-технического прогресса А. Показатели являются коэффициентами частной эластичности объема производстваY соответственно по затратам капитала K и труда L. Это означает, что при увеличении затрат капитала(труда) на 1% объем производства увеличивается на %().

Сумма коэффициентов является важным экономическим показателем, который носит название отдача от масштаба. При>1 – возрастающая отдача от масштаба(увеличение объема выпуска больше увеличения затрат ресурсов). При <1- убывающая отдача от масштаба (увеличение объема выпуска меньше увеличения затрат ресурсов). При говорят о постоянной отдаче от масштаба( во сколько раз увеличиваются затраты ресурсов, во столько же раз увеличивается выпуск)

47.Содержательная интерпретация коэффициентов полулогарифмических и логарифмических моделей регрессии

Полулогарифмическая модель:

Модель используется обычно в тех случаях, когда необходимо исследовать, как процентное изменение независимой переменной влияет на абсолютное изменение зависимой переменной. Так, например, если y=ВНП, а x=М, получим ВНП=Из данной формулы следует, что увеличение предложения денег М га 1% ведет к росту среднего значения ВНП на 0,01

48. Коэффициенты эластичности и их использование в эконометрическом анализе

Коэффициент эластичности представляет собой показатель силы связи фактора xг с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1 %. Коэффициент эластичности (Э) рассчитывается как относительное изменение у на единицу относительного изменения x:

Различают обобщающие (средние) и точечные коэффициенты эластичности. Обобщающий коэффициент эластичности рассчитывается для среднего значения :и показывает, на сколько процентов изменитсяу относительно своего среднего уровня при росте х на 1 % относительно своего среднего уровня. Точечный коэффициент эластичности рассчитывается для конкретного значения х = х₀: и показывает, на сколько процентов изменитсяу относительно уровня у(х₀) при увеличении х на 1% от уровня х₀. В зависимости от вида зависимости между х и у формулы расчета коэффициентов эластичности будут меняться. Основные формулы приведены в табл. 1.

Таблица 1

Вид функции y = f(x)	Точечный коэффициент эластичности	Средний коэффициент эластичности
Линейная y = b₀ + b₁
Парабола y= a + bx + cx²
Равносторонняя гипербола y = a + b/x
Степенная y=ax^b	Э(x₀) = b
Показательная y=ab^x

Только для степенных функций y=a·x^bкоэффициент эластичности представляет собой постоянную независящую отхвеличину (равную в данном случае параметруb). Именно поэтому степенные функции широко используются в эконометрических исследованиях. Параметрbв таких функциях имеет четкую экономическую интерпретацию – он показывает процентное изменение результата при увеличении фактора на1%. Так, если зависимость спросауот ценpхарактеризуется уравнением вида: y=200p^-1,5, то, следовательно, с увеличением цен на1%спрос снижается в среднем на1,5%. Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, бессмысленно определять, на сколько процентов изменится заработная плата с ростом возраста рабочего на1%. В такой ситуации степенная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наибольшего значенияR²), не может быть экономически интерпретирована.

Или лучше это

http://www.e-reading-lib.org/chapter.php/1002275/48/Yakovleva_Angelina_-_Otvety_na_ekzamenacionnye_bilety_po_ekonometrike.html

В общем случае коэффициент эластичности рассчитывается по формуле:

–первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня если факторная переменнаях изменится на 1 % относительного своего среднего уровня . Общая формула для расчёта коэффициента эластичности для среднего значения

факторной переменной х:

–значение функции у при среднем значении факторной переменной х. Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам. Для линейной функции вида: yi=, средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:

Для линейной функции вида: yi=, точечный коэффициент эластичности определяется по формуле:

Для показательной функции:

Для степенной функции:

studfiles.net

48. Коэффициенты эластичности

В общем случае коэффициент эластичности рассчитывается по формуле:

где

– первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

если факторная переменная х изменится на 1 % относительного своего среднего уровня

Общая формула для расчёта коэффициента эластичности для среднего значения

факторной переменной х:

где

– значение функции у при среднем значении факторной переменной х.

Для линейной функции вида:

yi=β0+β1xi,

средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Это единственная нелинейная функция, для которой средний коэффициент эластичности

равен коэффициенту регрессии β1.

Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:

Для линейной функции вида:

yi=β0+β1xi,

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение линейной функции в точке х1.

Для полиномиальной функции второго порядка (параболической функции) вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение параболической функции в точке х1.

Для показательной функции вида:

точечный коэффициент эластичности определяется по формуле:

Для степенной функции вида:

точечный коэффициент эластичности определяется по формуле:

Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

через первую производную результативной переменной по заданной факторной переменной x1:

Следовательно, Э(x1) = β1, что и требовалось доказать.

studfiles.net

Тема 6. Эластичность спроса и предложения Вопросы

Вопросы 1

1. Эластичность. Коэффициент эластичности 1

2. Прямая и перекрестная эластичность спроса по цене 2

3. Эластичность спроса по доходу 3

4. Эластичность предложения по цене 4

Основные понятия и категории:

Эластичность. Коэффициент эластичности. Точечная эластичность. Дуговая эластичность. Абсолютная эластичность. Абсолютная неэластичность. Единичная эластичность. Прямая эластичность спроса по цене. Факторы эластичности спроса по цене. Перекрестная эластичность спроса по цене. Товары-субституты. Товары-комплементы. Индифферентные товары. Прямая эластичность спроса по доходу. Аномальные товары. Нормальные товары. Эластичность предложения по цене. Факторы эластичности предложения. Эластичность предложения в кратчайшем, краткосрочном и длительном периодах.

1. Эластичность. Коэффициент эластичности

Способность спроса и предложения изменяться под влиянием различных факторов называется их эластичностью. Эластичность – это чувствительность одной переменной к изменению другой переменной. Например, чувствительность величины спроса или величины предложения к изменению какой-либо из их детерминант (цены на товар, дохода потребителя и т.д.). Степень эластичности можно измерить с помощью коэффициента эластичности:

На практике применяются различные методы расчета коэффициента эластичности.

Метод точечной эластичности используется в том случае, когда выведена функциональная связь рассматриваемых факторов (например, функция спроса от цены). Эта зависимость характеризует относительное изменение одного фактора (например, объема спроса) при бесконечно малом изменении другого фактора (например, цены):

Метод дуговой эластичности применяется, когда практические наблюдения не позволяют выявить функциональную зависимость спроса и предложения, поэтому по статистическим данным рассчитывается коэффициент эластичности между двумя точками линии спроса или линии предложения:

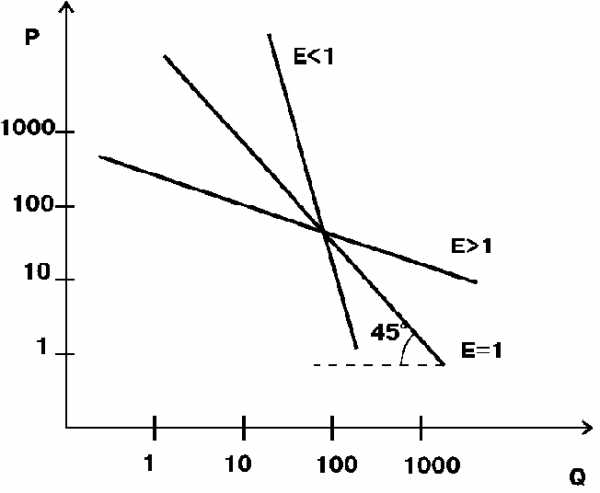
Если абсолютная величина коэффициента эластичности 0 < E < 1, то говорят о неэластичности спроса или предложения – темпы изменения рассматриваемого параметра меньше темпов изменения воздействующего на него фактора. Если Е = 1, то имеет место единичная эластичность – рассматриваемый параметр изменяется теми же темпами, что и воздействующий на него фактор. Если Е > 1, то спрос или предложение считаются эластичными – параметр изменяется более высокими темпами, чем изменяется влияющий на него фактор.

Кроме того, в теоретических моделях рассматриваются ситуации абсолютной неэластичности (Е = 0), когда изменение какого-либо параметра рыночной конъюнктуры вообще не оказывает влияния на величину рассматриваемого показателя, и ситуация абсолютной эластичности (Е = ∞).

Таким образом, эластичность характеризует чувствительность спроса или предложения к изменению каких-либо влияющих факторов. Степень чувствительности показывает коэффициент эластичности, который может рассчитываться точечным или дуговым методом.

2. Прямая и перекрестная эластичность спроса по цене

Коэффициент прямой эластичности спроса по цене показывает, на сколько процентов изменится величина спроса при изменении цены на 1 %. Эластичным спрос по цене бывает, как правило, для предметов роскоши и достаточно дорогих предметов потребления (автомобили, телевизоры, стиральные машины, аудио- и видеотехника, персональные компьютеры и др.). Неэластичен спрос, как правило, на товары первой необходимости с относительно низкими ценами (хлеб, картофель, одежда, обувь и пр.).

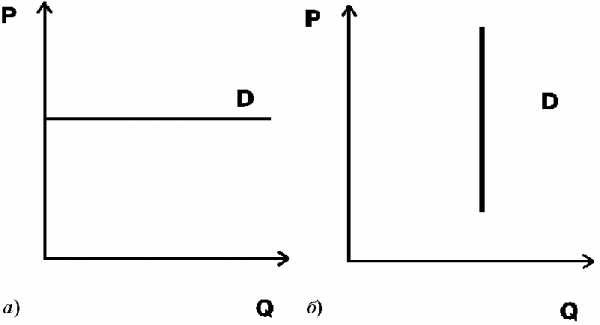
Рисунок 6.1 – Эластичность спроса

Чем выше коэффициент эластичности, тем более полого расположена линия спроса (см. рис. 6.1).

В случае абсолютно эластичного спроса — это горизонтальная кривая спроса (рис. 6.2 а) — потребители платят одну и ту же цену за товар, невзирая на величину спроса.

В случае абсолютно неэластичного спроса они покупают одно и то же количество товара при любых уровнях цен. То есть изменение цены не вызывает никакого изменения спроса, а кривая вырождается в вертикальную прямую (рис. 6.2 б).

Рисунок 6.2 — Экстремальные случаи эластичности спроса

В качестве примера абсолютно неэластичного спроса можно рассматривать спрос на инсулин для больных сахарным диабетом (без него человек может умереть, а при правильном приеме нормально доживает до старости).

Абсолютно эластичный спрос характерен для ситуации совершенной конкуренции, когда производители не могут влиять на цену, а покупатели готовы приобретать любое количество товаров по данной цене.

Эластичность спроса по цене зависит от ряда факторов:

1) незаменимость — если у товара есть заменители (товары-субституты), то спрос будет более эластичным;

2) значимость товара для потребителя — неэластичным является спрос на товары первой необходимости, а более эластичным — на все другие группы товаров;

3) удельный вес в доходах и расходах — товары, на которые тратится значительная доля средств, — эластичны, а занимающие незначительную долю бюджета — неэластичны.

4) временные рамки — эластичность спроса увеличивается в долгосрочном периоде, так как покупатели располагают временем для подбора замены подорожавшему благу.

При изменении цен на товары с разной эластичностью выручка от реализации продукции меняется по-разному. При эластичном спросе снижение цены ведет к увеличению общей выручки (см. рис. 6.3 а). В случае единичной эластичности прирост объема продаж при снижении цены таков, что общая выручка остается неизменной (см. рис. 6.3. б). При неэластичном спросе снижение цены ведет к снижению общей выручки (см. рис. 6.3.в).

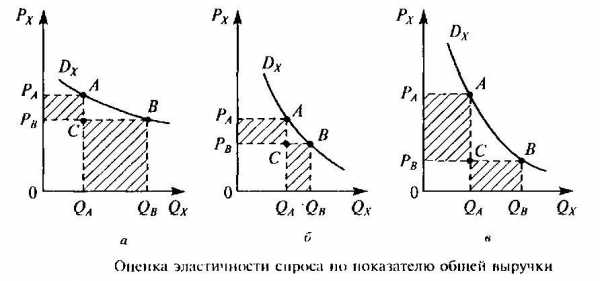
Рисунок 6.3 — Изменение выручки продавца при различной эластичности спроса

Коэффициент перекрестной эластичности спроса показывает степень количественного изменения спроса на товар А при изменении цены на товар В на 1 %:

Если Ecross > 0, то товары взаимозаменяемы (товары-субституты).

Если Ecross < 0, то товары являются взаимодополняющими (товары-комплементы)

Если Ecross = 0, то товары являются индифферентными друг к другу.

Таким образом, прямая эластичность спроса по цене, характеризующая степень изменения спроса при изменении цены на 1 %, зависит от ряда факторов и оказывает значительное влияние на изменение выручки от продажи продукции в ответ на изменение уровня цен. Перекрестная эластичность характеризует степень изменения спроса на один товар при изменении цены на другой товар на 1 %, что позволяет выделить товары-субституты, товары-комплементы и индифферентные товары.

studfiles.net

Эластичность в эконометрике

Сущность коэффициента эластичности

Коэффициент эластичности, как и индексы детерминации и корреляции для нелинейных форм связи, используются для характеристики зависимостей результативной и факторных переменных. Коэффициент эластичности позволяет дать оценку степени зависимости переменных.

Определение 1

Коэффициент эластичности – это показатель силы связи фактора с результатом, который показывает, как изменится значение результата в случае изменения на 1 процент значения фактора.

Замечание 1

Цель расчета коэффициента эластичности в эконометрике — показать относительное изменение анализируемого показателя при единичном относительном изменении экономического фактора, который на него влияет при неизменности остальных факторов.

Средние и точечные коэффициенты

Коэффициент эластичности может быть рассчитан как средний и точечный коэффициент.

Средний коэффициент эластичности показывает, на сколько процентов будет меняться результативная переменная относительно ее среднего уровня при изменении факторной переменной на 1 % относительно своего среднего значения.

Замечание 2

Средние показатели эластичности можно сопоставлять друг с другом, а, значит, ранжировать факторы в зависимости от силы их воздействия на результаты.

Точечный коэффициент эластичности характеризуется тем, что на эластичность функции влияет заданное значение факторной переменной.

Точечный коэффициент эластичности показывает, как изменится результативная переменная (в процентном выражении) относительно ее значения в определенной точке при изменении факторной переменной на 1 % относительно установленного уровня.

Применение коэффициента эластичности

Зачастую коэффициент эластичности используется при проведении анализа производственных функций. Вместе с тем, расчет коэффициентов эластичности не всегда будет иметь смысл, поскольку в ряде случаев невозможно или даже бессмысленно интерпретировать факторные переменные в процентном отношении.

Приведем примеры ситуаций, когда нет смысла рассчитывать коэффициент эластичности:

Ситуация, для анализируемых признаков нецелесообразно определять их изменение в процентном выражении. Примером может выступать задача по расчету относительного изменения заработной платы в случае увеличения стажа работы на определенной должности на 1%. В подобной ситуации определение правильной степенной функции не дает возможности ее экономически интерпретировать.
Еще один пример — изучение соотношения ставок межбанковского кредитования (в процентах годовых) и периода его предоставления в днях. В данном случае будет получено уравнение регрессии, которое характеризуется довольно высоким показателем корреляции. Расчет коэффициента эластичности не имеет смысла, поскольку срок межбанковского кредитования не может быть измерен в процентном выражении. Для подобной зависимости больший интерес для анализа представляет линейная функция, которая имеет более низкое значение показателя корреляции. Коэффициент регрессии позволяет дать оценку процентному изменению кредитных ставок при увеличении периода его предоставления на один день.

Для линейных моделей множественной регрессии, в которых факторные признаки различаются по своей сути или характеризуются различными единицами измерения, коэффициенты регрессии — несопоставимы. Исходя из этого, уравнение регрессии может быть дополнено соизмеримыми параметрами близости связи фактора и результата, которые позволяют проранжировать факторы в зависимости от силы влияния на результат.

spravochnick.ru

2.Величина коэффициента эластичности показывает:

Тест: Ответы на тест по эконометрике

48. Коэффициенты эластичности. Ответы на экзаменационные билеты по эконометрике

46.Содержательная интерпретация коэффициентов степенной регрессионной модели

47.Содержательная интерпретация коэффициентов полулогарифмических и логарифмических моделей регрессии

48. Коэффициенты эластичности и их использование в эконометрическом анализе

48. Коэффициенты эластичности

Тема 6. Эластичность спроса и предложения Вопросы

1. Эластичность. Коэффициент эластичности

2. Прямая и перекрестная эластичность спроса по цене

Эластичность в эконометрике

Сущность коэффициента эластичности

Средние и точечные коэффициенты

Применение коэффициента эластичности

Добавить комментарий Отменить ответ